Manacher算法(马拉车)

Manacher也是一种字符串算法，是可以查找一个字符串的最长回文子串的线性算法

先说一下什么回文子串，子串的意思就该字符串中任意个连续的字符组成的子序列，对于字符串”abbac”，”abb”就是子串，但是”aba”不是因为不连续，那回文串简单的就是说正着读和反着读都是一样的字符串，那么这俩一结合就是回文子串的意思

暴力算法

对于一个问题我想试着去想一下暴力怎么解决，有助于帮助我们理解算法，因为这些算法就是暴力算法的优化版本，暴力做法就很简单，

我们枚举出每个子串然后暴力判断他是不是回文串，枚举每个子串时间复杂度是O(N2)，判断则是O(N)，那暴力的时间复杂度就是O(N3)，

拿这个复杂度很高的，但是这个就太暴力了，有稍微优化一点的就是去枚举中心，然后从中心向外扩展判断回文串，但是因为如果字符串的中心会因为长度奇偶性改变所以要特判一下奇偶性，具体代码就不展示了，大概知道就行，主要看接下来的

奇数情况

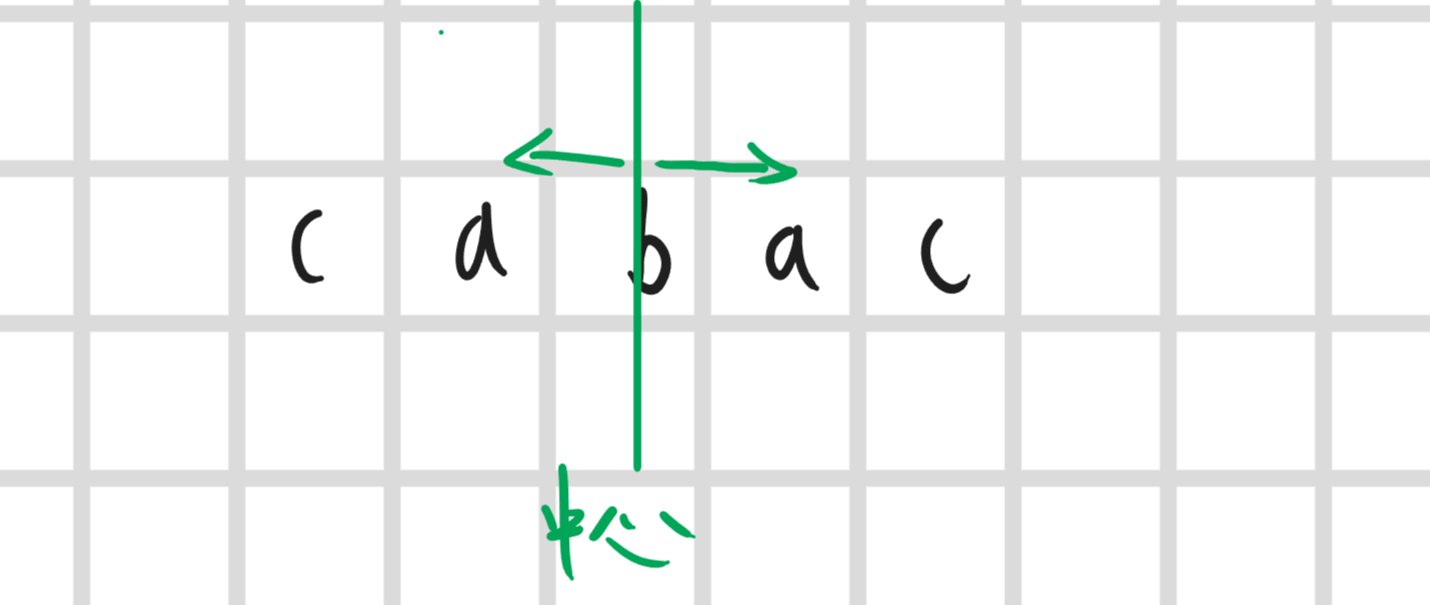
image.png

偶数情况

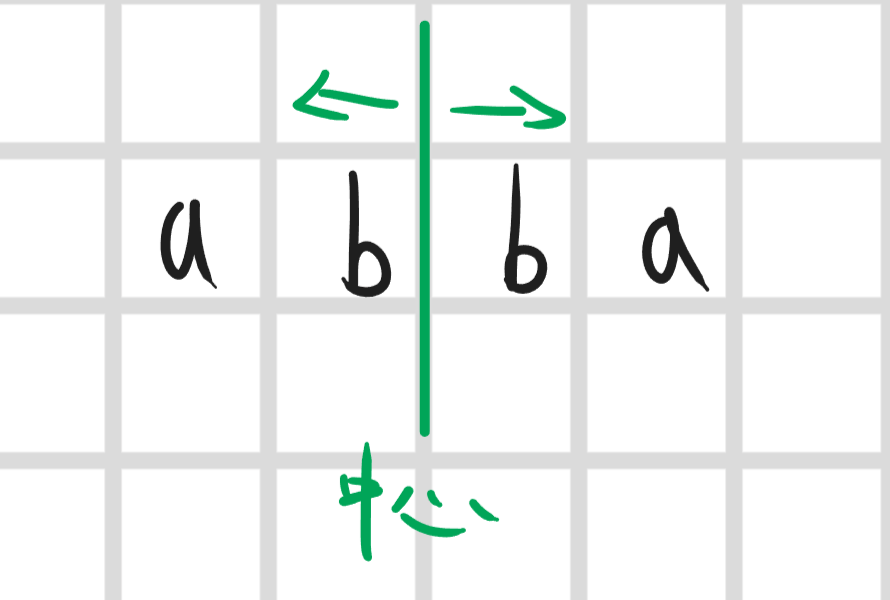
image.png

Manacher算法原理

对于刚刚优化的暴力算法，因为他需要判断奇偶性很麻烦，所以我们根据原串重新构造，对于一个字符串S”ababababa”，在字符串开头结尾以及每个字符中间插入一个原串没有出现过的相同字符，如下所示：

下标： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
元素 # a # b # a # b # a # b # a # b # a #

这么操作的话，会发先字符串不管是奇数还是偶数构造后都是奇数，并且给每一个回文串都给了一个中心，奇数长度回文串本身就有中心，偶数长度回文串中心其实不存在是空隙(看上图)，但是我们构造会在两个字符之间插入新的字符所以相当于赋予了中心

优化暴力做法是从中心向外扩展求得以这个字符为中心的回文子串长度，然后就可以找到最长的回文子串，也就是说以每个字符为中心的最长回文子串我们是都可以知道的，但是暴力优化做法每次中心扩展都是一个一个扩展，这样就会很慢，所以Manacher算法就是想我能不能一次多扩展一些不是一个一个来，什么意思呢，比如上面那个字符串s”ababababa”

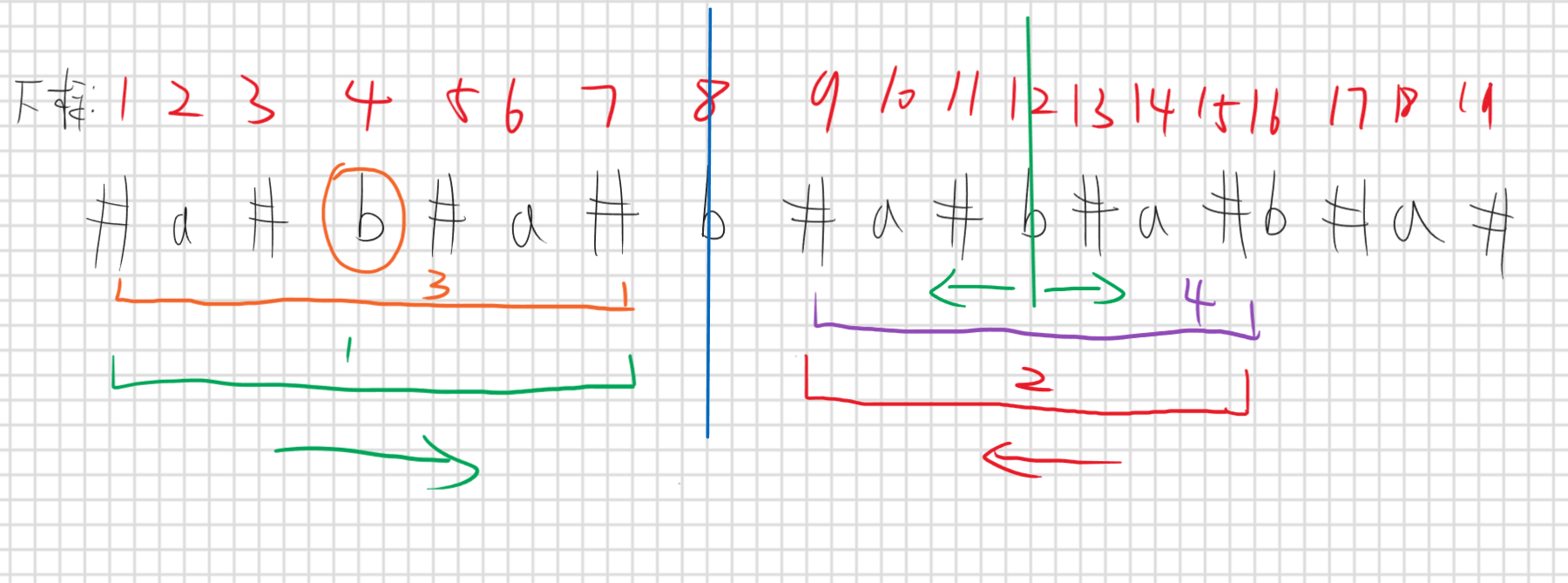
image.png

假如我们现在中心枚举到s[12]也就是那条绿色竖线，按照暴力做法我们是一个一个向外扩展，但是我们能否根据已知信息使得我们可以一次多扩展几步呢，当枚举到s[12]中心是，前面所有的中心我们都处理过了，也就是说以s[1,11]字符为中心的最长回文串我们已经求出来，那这些可以给我们提供那些信息呢，我们看以s[8]为中心(不要在意为什么是8不是其他后面会解释)，那因为我们已经求出来以s[8]为中心的最长回文子串，也就是s[1,15]，也就是说区间1=区间2(因为回文，但是注意区间1是从左往右看，区间2是从右往左看)，因为s[12]包含在以s[8]为中心的回文子串中，又因为s[12]在区间2中，所以区间1的s[4]一定等于s[12]，那同样的以s[4]为中心的最长回文子串我们也求出来了，那么既然区间1和区间2相同，那是不是说以s[4]为中心的最长回文子串一定也是以s[12]为中心的回文子串(假设以s[4]为中心的回文子串没用超出区间1)，所以我们在求以s[12]为中心的回文子串不需要一个一个扩展了，可以直接扩展成s[4]的最长回文子串，然后继续向外扩展，如果s[4]的最长回文子串长度超过区间1，那s[12]的回文子串只能先扩展成在区间1的那一段回文子串。

Manacher其实就是这个思想，就是根据之前的已知信息推出后面的，利用这些已知的我们就不需要一次一次扩展了，最终达到线性时间复杂度

回文半径

那我们刚刚也说了在求以s[i]字符为中心的最长回文半径的时候，以s[1,i-1]这些字符为中心的最长回文子串已经求出来了，所以我们需要把他们存一下，存什么呢也就是回文半径，我们把回文半径存在一个数组Len

Len[i]的意思就是说，以s[i]字符为中心的最长回文半径长度，回文半径长度就是回文子串长度/2+1，也就是说s[i-Len[i]+1,i+Len[i]-1]是以s[i]为中心的最长回文子串

并且Len[i]-1就是原串得最床回文子串长度，因为你扩展完的回文串中原串字符数量如果是n，那么’#’数量就是n+1(因为插空，头尾放)，

扩展后的回文串长度为n+n+1=(Len[i])*2-1=2Len[i]-1，那么n=Len[i]-1

Manacher流程

大体Manacher讲了，但是刚刚其实有一个遗留问题，那就为什么处理Len[12]是是去看Len[8] (原理那里举的例子)，明明1到11我们都求出来了为啥非得是8呢

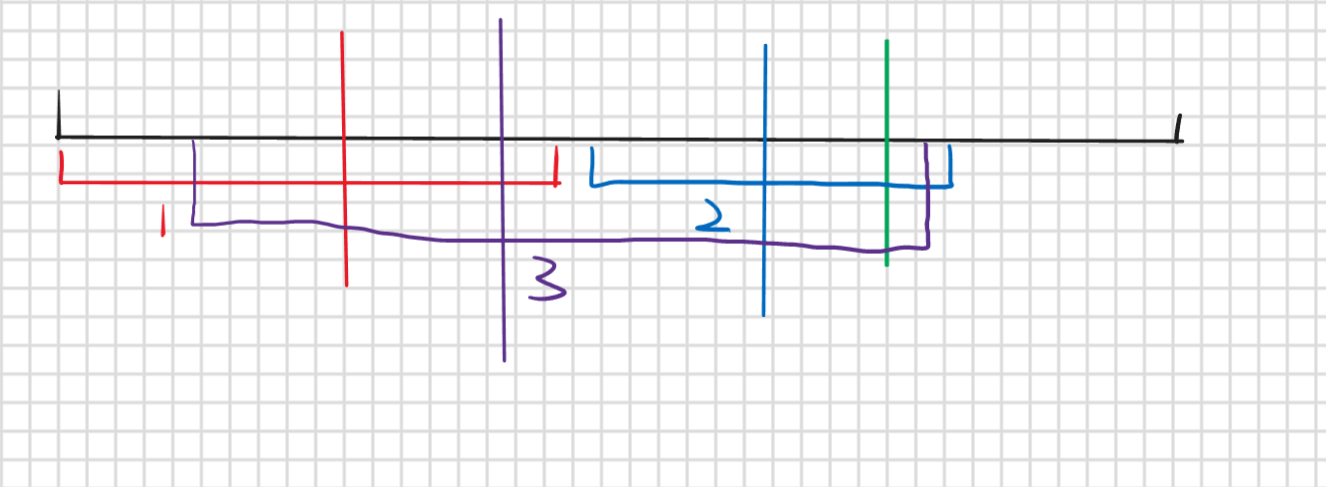
image.png

考虑这么一个问题，假如我们要求的是绿色竖线为中心的最长回文子串，其他颜色竖线分别是他们的中心，对应颜色区间就是以他们为中心的回文子串，他们都可以提供信息，那谁提供的最有效呢，是覆盖区间最长的还是左边界最左还是右边界最右呢，结论是最长回文子串右边界最右的哪个能提供最有效的信息，为什么呢，回想我们刚刚那个过程，我们求最长回文子串从中心向外扩展的时候一次一次来太慢了，就希望能多扩展几个，那我如何知道我能扩展多少个呢，是因为要求的中心他被包含在了之前所求的回文子串中，对应到图就是绿色被包含在了区间2和区间3，区间1则没有用，因为只有被包含在回文区间，我们就可以找到与之对应的中心，那对应的中心的最长回文子串长度，也就是我们要求的回文子串长度（但不是最长，不理解就再看看上面哪个原理举得例子，现在是抽象的讲不是很好理解可能），

所以哪个回文子串提供的信息最多呢，那就是右边界最右的，右边的那些中心的回文子串我们还没求左边的都求了，哪个回文子串包含越多没求的中心，他就能提供更多的信息，所以我们记录一下这个提供最多信息的区间和，它所对应中心

然后就看代码吧

代码

Manacher模板题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>
#include<string.h>
using namespace std;
typedef long long ll;
const int N =1e7+1e6+5;
char s[N],tmp[N<<1];
int Len[N<<1];
int init(char *str){//构造字符串
	int cou=0,len=strlen(str);
	tmp[cou++]='$';//最开头插入一个从没出现过的字符，因为这是字符串左尽头这样当你匹配到它的时候一定失败，所以不会出现越界，不					//然每次到0点还要判断一下
	for(int i=0;i<len;i++){
		tmp[cou++]='#';		//开头和结尾以及每个字符之间都插入一个更其他都不一样的字符，但插入的这个是一样的只是跟其他不一样
		tmp[cou++]=str[i];	//放入原串
	}
	tmp[cou++]='#';
	//结尾也可以跟头哪个一样插入一个避免越界但是因为字符串其实会自动插入一个'/0'所以无所谓
	return 2*len+1;//返回构造后字符串长度 构造后的字符串大概长这样"$#a#b#a#" 
    
}

int Manacher(char *str){
	int len=init(str);//构造字符串
	int mx=0,p=0,ans=0;//mx是回文子串覆盖最右的哪个回文子串能覆盖到的最远距离，p就是哪个最远哪个回文子串的中心
	for(int i=1;i<=len;i++){//枚举中心
		if(i<mx){//如果当前中心被覆盖了，那么我们就可以根据已知信息，去更新Len[i]，而不是一个一个扩展
			Len[i]=min(mx-i,Len[2*p-i]);//看下图
		}
		else{//没有覆盖那就只能是1了呗
			Len[i]=1;
		}
		while(tmp[i-Len[i]]==tmp[i+Len[i]]){//因为可能还可以继续扩展所以暴力扩展
			Len[i]++;
		}
		if(i+Len[i]>mx){//如果以tmp[i]为中心得最长回文子串比之前那个覆盖的还远那就更新
			mx=i+Len[i];
			p=i;
		}
		ans=max(ans,Len[i]-1);//更新ans
		
	}
	return ans;//最后ans就是该字符串得最长回文子串长度
	

}

int main(){
	
	scanf("%s",s);
	cout<<Manacher(s);

	return 0;
}

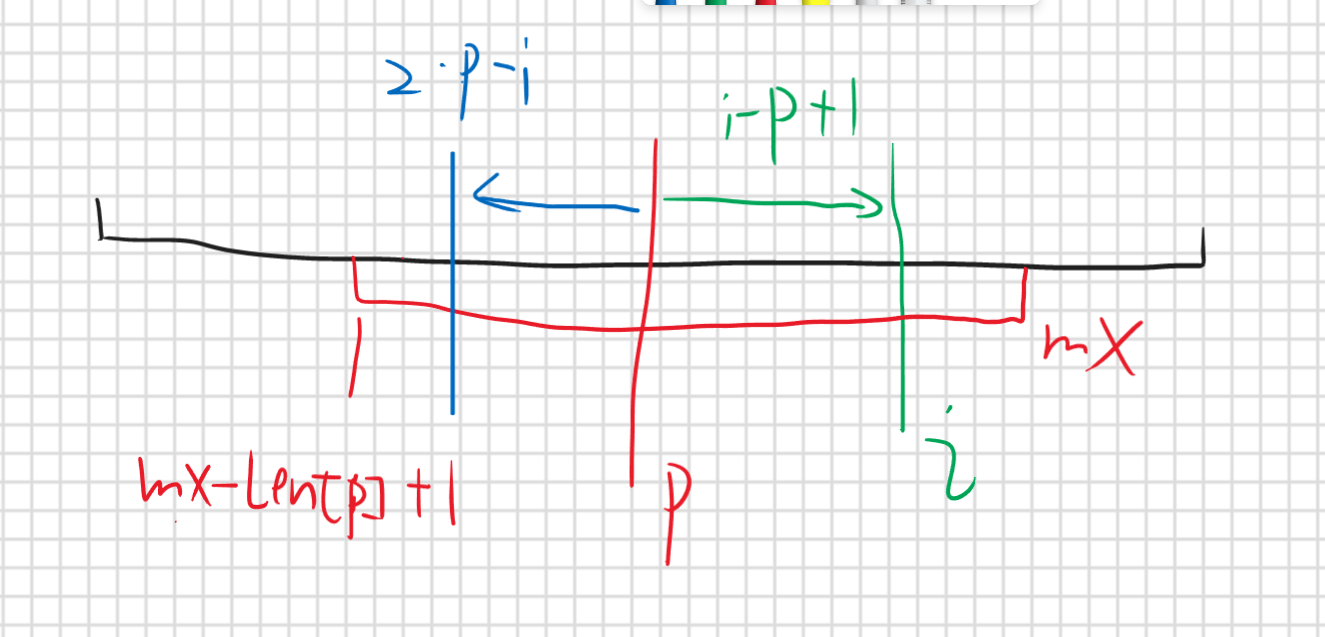
image.png

1
Len[i]=min(mx-i,Len[2*p-i]);

求得是以s[i]为中心得最长回文子串，mx是前面s[1,i-1]为中心得能覆盖的最远距离，p就是对应得那个中心，所以红色区间就是以p为中心得最长回文子串，且它覆盖距离最远也就是最右，如果s[i]在mx以内那就说明被覆盖，因为回文那么那就能在p得回文子串左半边找打一个与之对应得相同得字符，并且他的最长回文子串也是s[i]得回文子串，那对应的那个中心的下标就是2*p-i，但是可能这个中心得最长回文子串超过了p覆盖的范围，所以取了一下最小值，然后更新Len[i]