KMP算法理解分析

KMP本质就是一种字符串匹配算法，字符串匹配是什么呢，举个例子，有一个字符串”abbabcda”(一般称为主串)中去看另一个字符串”abc”(一般称为目标串)是否存在，就是一种字符串匹配问题

暴力字符串匹配

对于上述问题我们先用最简单的暴力算法去解决，就是去从左到右一个一个去匹配，如果有某个字符匹配不成功，那么目标串就往右移动一位，然后重新从左到右一个一个匹配，直到匹配成功，那就说明主串中存在目标串，或者主串遍历完都没有匹配成功那就说明主串中不存在目标串

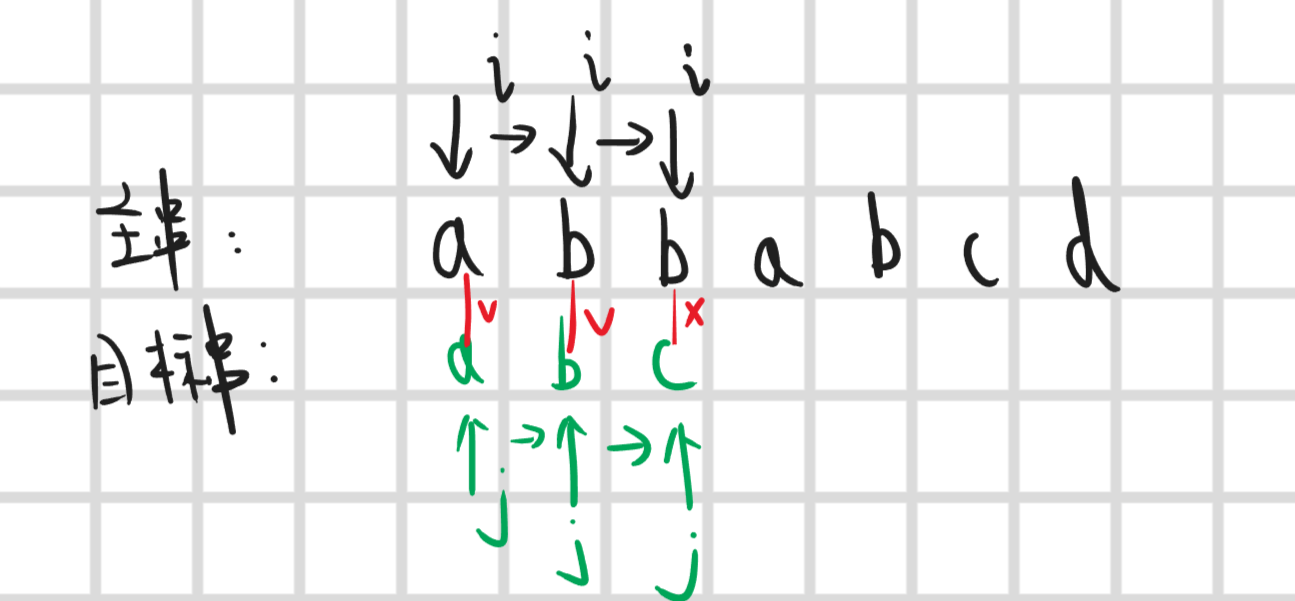
image.png

image.png

暴力思路不难，看一下代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N =1e6+5;

char s[N],p[N];//s是主串，p是目标串 

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);

	scanf("%s",s+1);
	scanf("%s",p+1);
	int i=0,j=0;
	int lena=strlen(s+1);
	int lenb=strlen(p+1);
	bool flag;
	for(int i=1;i+j-1<=lena;i++){
		flag=true;
		for(int j=1;j<=lenb;j++){
			if(s[i+j-1]!=p[j]){
				flag=false;
				break;
			}
		}
		if(flag==true)break;
	} 
	if(flag)cout<<"YES";
	else cout<<"NO";

	return 0;
}

那这个时间复杂度就是O(NM)，是很高的

KMP算法

暴力算法为什么慢呢，是因为他每次匹配失败后都只是目标串右移一位，然后从头开始重新匹配，那KMP的思路就是说我匹配失败的时候能不能多移动几位且不影响正确性，举个例子主串S “ababc”，和目标串P “abc”，下标从1开始

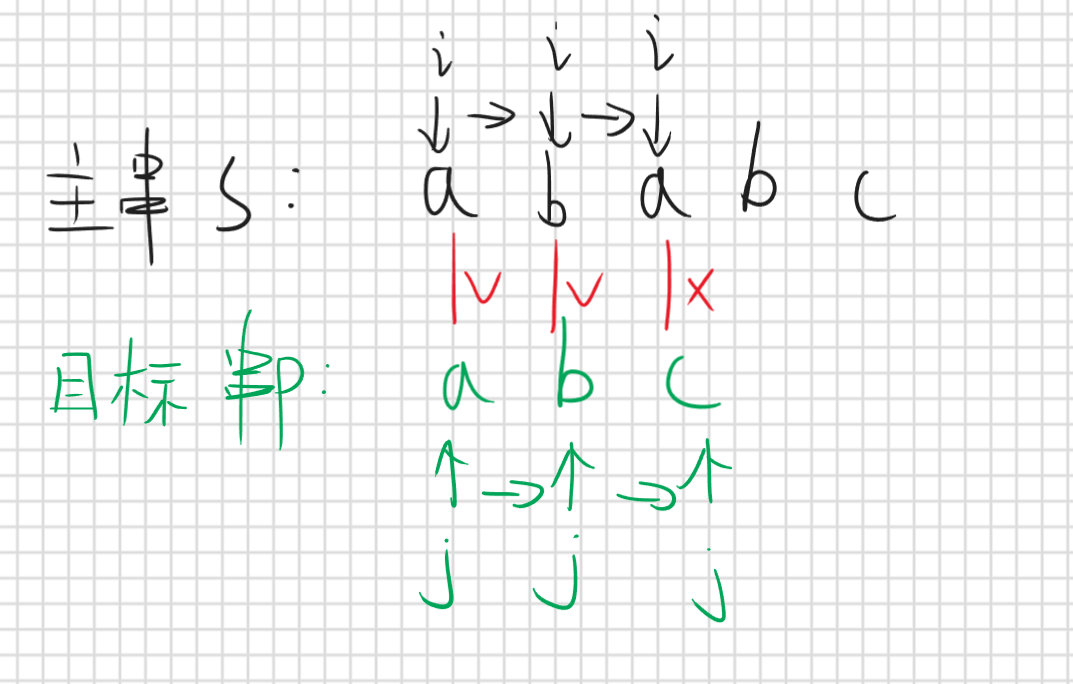
image.png

当匹配到第三位是s[3] (‘a’) != p[3] (‘c’) ，这时候匹配失败了暴力做法是目标串右移一位，但是我们根据目标串的信息知道p[1]!=p[2]，但是主串和目标串的前两位已经匹配成功，那就说明p[1]==s[1]并且p[2]==s[2]，那么因为p[1]!=p[2]那么p[1]!=s[2]，那么就没必要右移一位，因为根据我们已知的信息知道当前情况右移一位一定不会匹配成功，所以我们可以右移两位，因为右移两位我们不确定他是不是错的，但是右移一位一定是错的，所以右移两位后继续匹配看能否成功

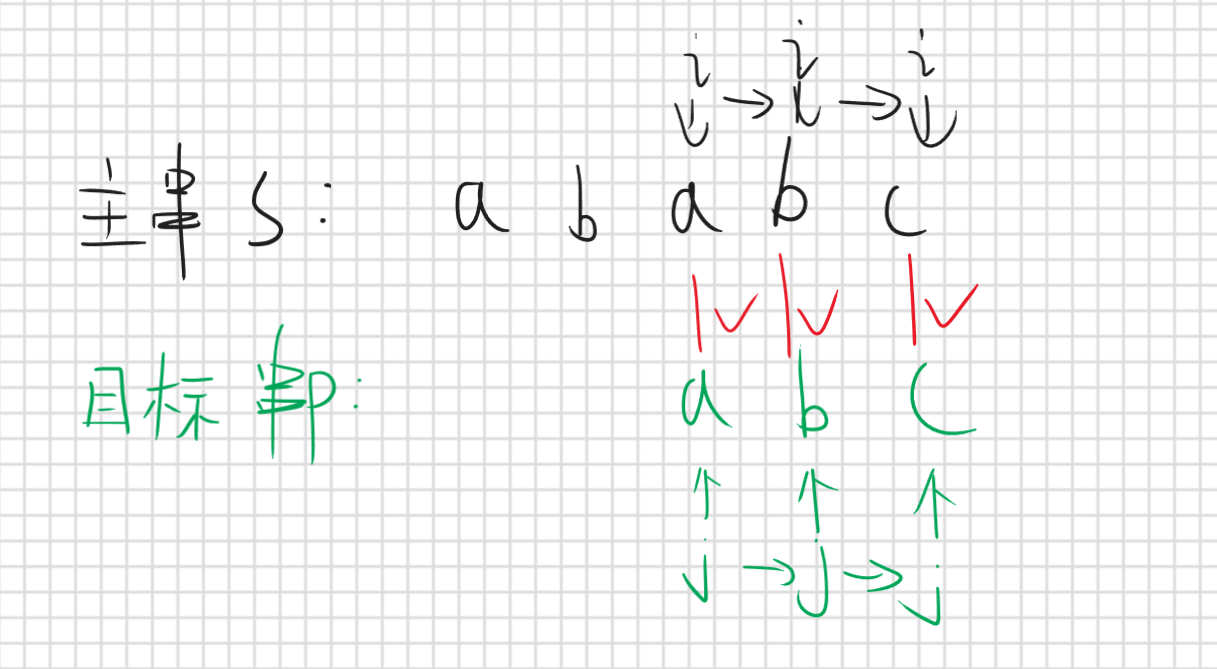
image.png

这就是KMP的思想，我们想尽可能多移动几位，并保证正确性，也就是根据目标串和已经匹配成功的字符所产生的信息去判断移动那些位一定是不对的，移动到哪里是最优的。

那这里需要先引入一个概念叫做最长公共前后缀子串，比如一个字符串”aba”，子串的意思就该字符串中任意个连续的字符组成的子序列，前缀子串就是说这个子串必须由s[1]开始（假设下标从1开始），后缀则是必须由s[n]结束(n为字符串长度)，公共前后缀子串就是说这个字符串的相同的前后缀子串，这个字符串有一个前缀子串”a”，后缀子串”a”，然后这俩相等那么”a”就是公共前后缀子串，最长就是说最长的呗

那回到刚刚的问题，我们怎么根据已知信息去移动到一个尽可能远且保证正确的位置呢，举个例子主串S”ababc”，目标串P”abac”

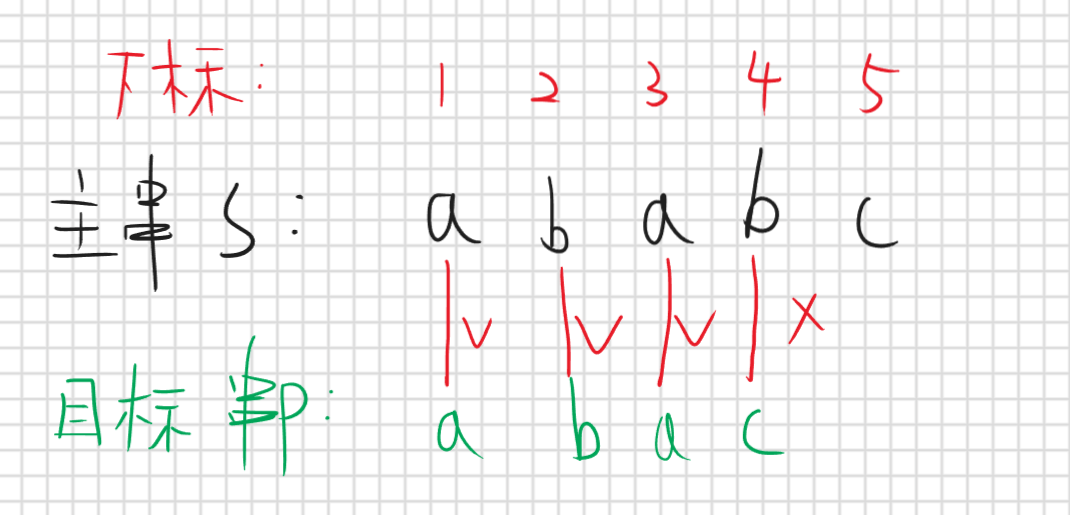
image.png

先按照暴力匹配到第四位是匹配失败，这时候该右移多少位才最优呢，首先我们目前有哪些信息呢，我们知道目标串所有字符，并且我们知道主串和目标串前三位已经匹配成功，第四位失败，如果右移一位可以吗，可以但没必要，因为根据已知信息我们是可以知道s[2]!=p[1] (就跟上面说的那个一样)，那右移两位呢

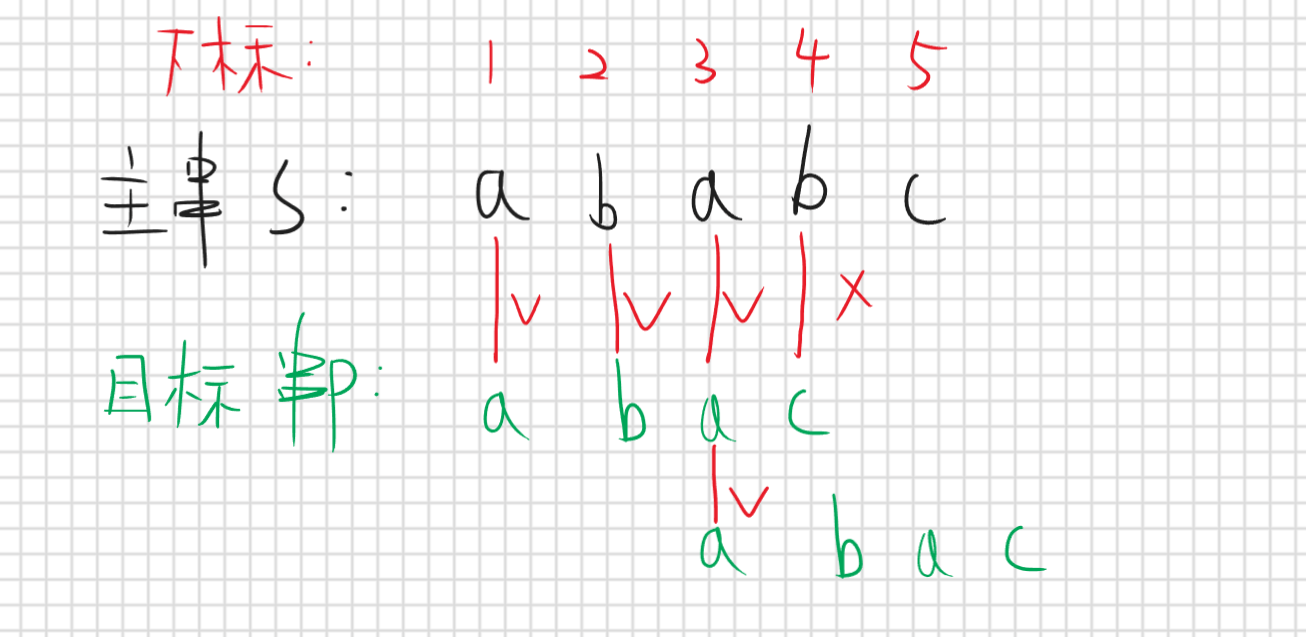
image.png

我们发现移动两位是可以的，就什么意思呢，因为根据目标串我是可以知道p[1]==p[3] (先不要管咋知道的)，并且前三位s和p是相同的，那么移动两位后，是p[1]正好对应的就是s[3]那么根据我们已知信息知道他们是相同的，那我们看一下这个到底是个啥，我们移动两位后，p[1]跟s[3]匹配成功，p[1]是不是目标串p的前缀子串，s[3]也就是p[3]（因为前三位相同）是不是就是后缀子串，那这俩相同是不是就说明这俩就是公共前后缀子串，那我们这里可以先下个结论如果第j位匹配失败那么移动的位置就是移动到前j-1位字符串的最长公共前后缀子串这就是正确的，什么意思呢，刚刚举的都是实际列子，下面要抽象化去证明这个结论

证明

结论：当第s[i]和p[j]匹配失败时，去找p[0,j-1]所代表的子串的最长公共前后缀子串，然后前缀移动到后缀

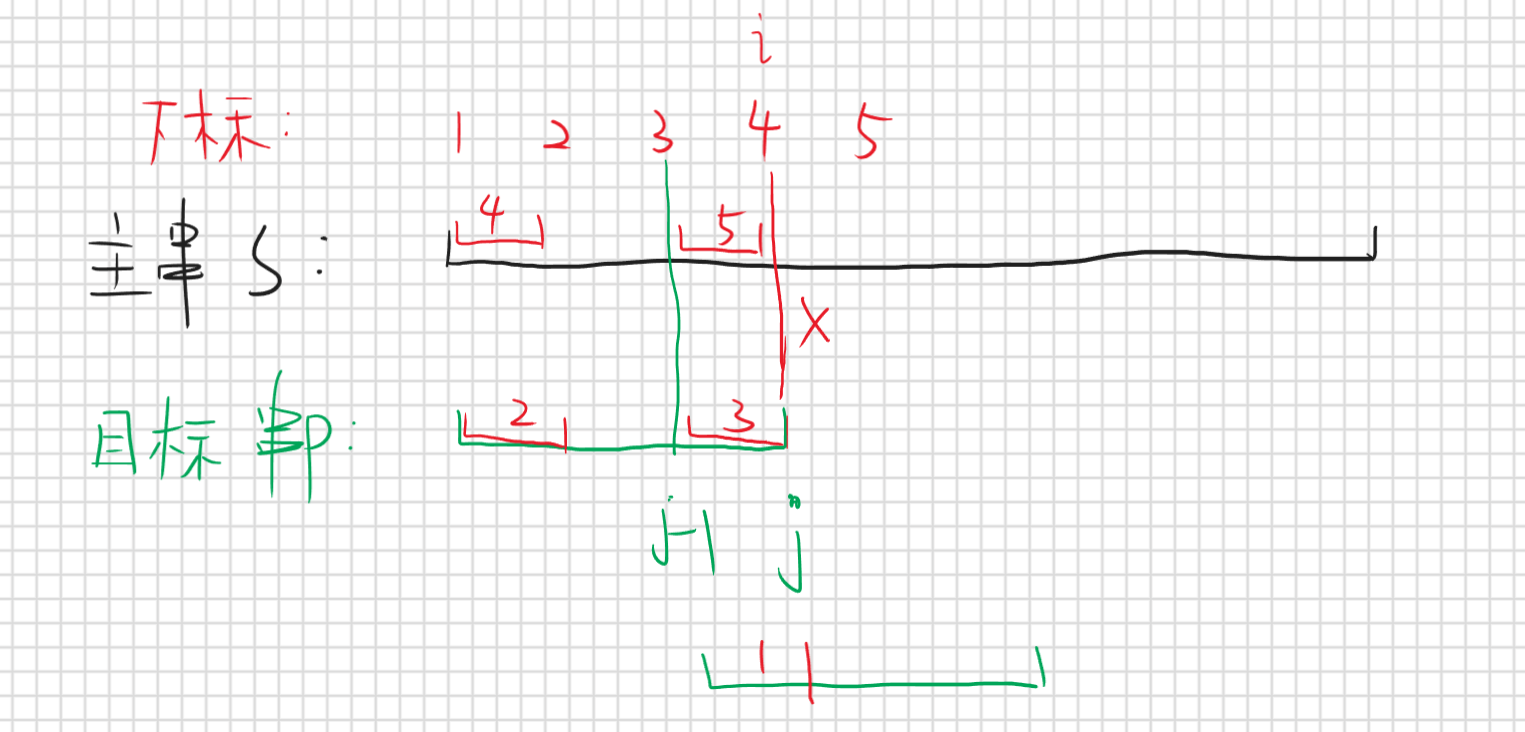
image.png

区间2表示的就是p[0,j-1]子串的最长公共前后缀子串的前缀子串，区间3则是后缀子串，所以区间2=区间3，区间4，5是与之对应的属于s的前后缀子串，因为前j-1位匹配成功所以区间2=区间3=区间4=区间5，区间1就是区间2，解释一下结论就是说当s[i]!=p[j]是找当p[0,j-1]的最长公共前后缀子串，也就是区间2和区间3，然后移动目标串p，移动到区间1(也就是公共前后缀字串的的前缀子串)对着区间3(后缀子串)

按照暴力做法肯定是对的，因为是一位一位去比的，那我们一下跳了那么多位怎么保证跳过去的一定是错的呢，那我用反证法去证明，假设我们跳过存在正确匹配的情况

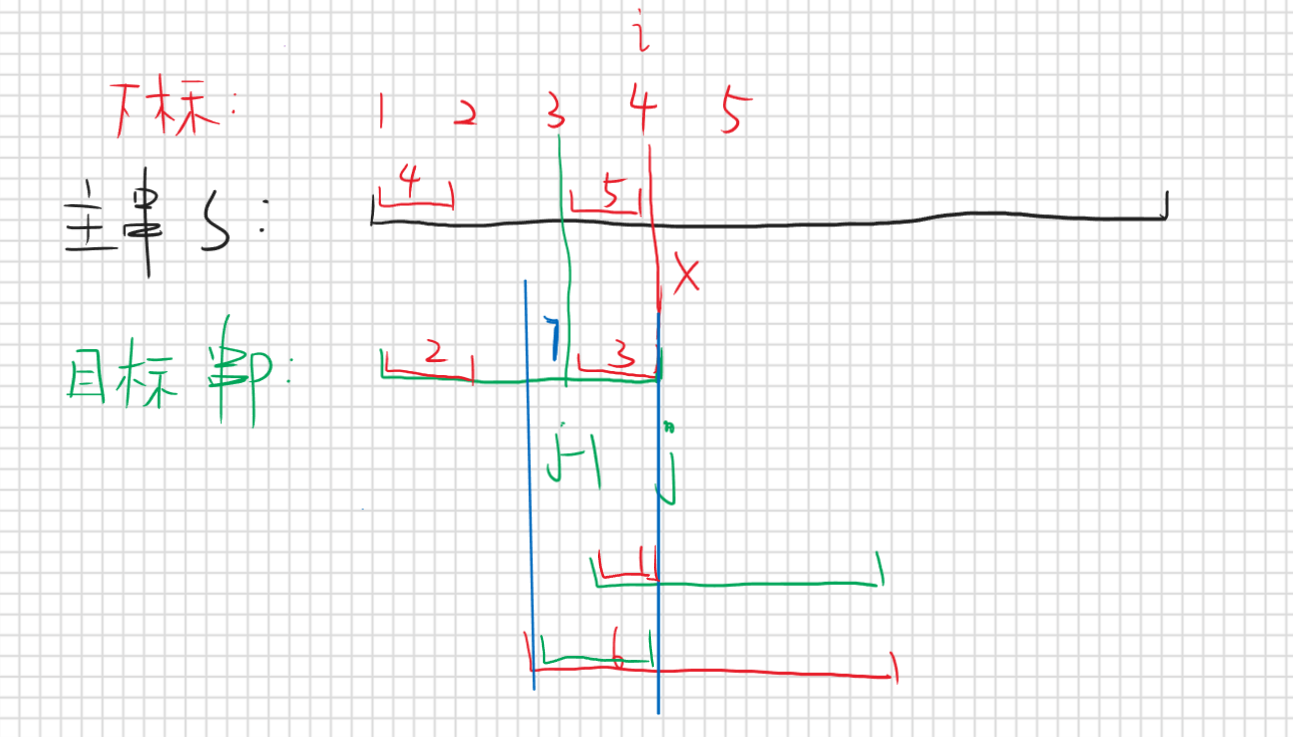
image.png

按照假设说明那么最下面那条红线就是一种跳过的情况假设他是正确匹配的，那么区间6就应该等于区间7(蓝色分割的区间)，但是区间6本身就是目标串p的前缀子串，而区间7也是目标串的后缀子串，那他俩既然相等，且很明显区间6长度比区间1长，那么最长公共前后缀子串应该是6而不是1，那么我们就应该移动到区间6这个位置而不是区间1那么就矛盾了，假设也就不成立，所以我们的结论是正确的，也就是说根据最长公共前后缀子串的信息我们可以确定在最长公共前后缀子串之前的那些位置一定是不能匹配成功的否则他们才是最长公共前后缀子串，那为什么要移动到最长的呢，我多移动一位行不行呢，那肯定是不行的，因为对于最长公共前后缀子串这个位置，是正确性未知的，我们只知道前面都是错的，但是后面的都不知道，所以只能从这里开始继续匹配。

Next数组

那KMP的思路就已经大概知道了，目前的问题就变成怎么去求解这个最长前后缀公共子串了，根据观察我们发现只需要求出目标串的每一个长度对应的最长公共前后缀子串长度就行，这就是Next数组，Next[i]的意思就是目标串子串P[1,i]（下标从1开始）对应的最长公共前后缀子串长度

那么求出来这个之后就可以去写代码了，先不管咋求出来的Next数组我们先看整体的一个代码逻辑后面再讲咋求的

代码(不包含Next数组实现)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<map>
using namespace std;
const int N =1e6+5;
char p[N],s[N];
int Next[N]; 
int main(){
	ios::sync_with_stdio(false);
	int n,m;
	cin>>n>>p+1>>m>>s+1;//p是目标串 s是目标串 下标从1开始

	//kmp
	bool flag=true;
	for(int i=1,j=0;i<=m;i++){//i表示的是主串的那个指针，j表示的是目标串那个指针，接下来的比较是s[i]和p[j+1]比较
		while(j&&s[i]!=p[j+1])j=Next[j];//匹配失败移动J指针到合理位置也就是公共前缀移动到后缀
        //如果移动一次发现还是匹配失败那就继续移动到移动后的子串的公共前后缀子串，直到匹配成功或者j为0
        //j表示的其实就是成功匹配过的前面的子串既然为0了那也就没有可用信息了
		if(s[i]==p[j+1])j++;//如果匹配成功指针就右移一位
		if(j>=n){//完全匹配成功也就是找到目标串
			flag=false;
			cout<<i-n<<' ';
			j=Next[j];
		}
	} 
	
	if(flag) cout<<-1<<endl;
	

	return 0;
}

Next数组实现

Next数组其实和kmp代码差不多，就是相当于是自己和自己匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<map>
using namespace std;
const int N =1e6+5;
char p[N],s[N];
int Next[N]; 
int main(){
	ios::sync_with_stdio(false);
	int n,m;
	cin>>n>>p+1>>m>>s+1;
	//求Next数组 Next[i]长度为i的模板串子串的公共前后缀字串长度 
    //Next[0]没有意义，Next[1]因为子串不能比原串大，所以只能是0也不需要处理直接从2开始
   	//j表示的是对于i来说就是Next[i-1]，初始为0
	for(int i=2,j=0;i<=n;i++){
		while(j&&p[i]!=p[j+1])j=Next[j];//看下图
		if(p[i]==p[j+1])j++;
		Next[i]=j;
	}

	

	return 0;
}

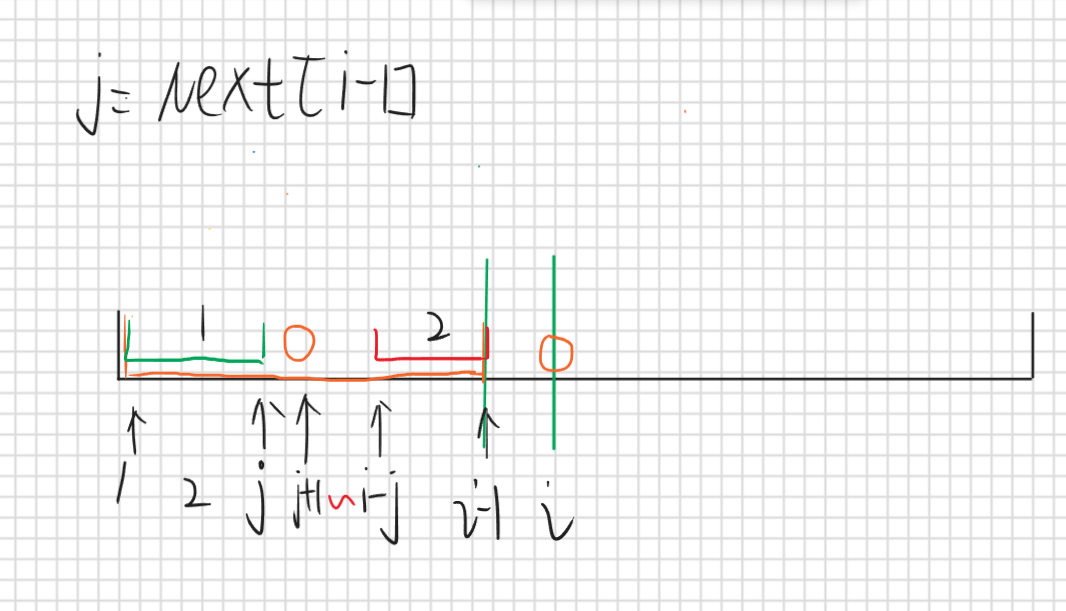
image.png

对于求Next[i]的值我们发现只需要直接比较p[j+1]和p[i]即可，首先j表示的是Next[i-1]也就是前i-1位的最长公共前缀子串长度，那么p[1,j]==p[i-j,i-1]，那么如果p[j+1]==p[i]那就说明p[1,j+1]==p[i-j,i]那这就是最长前后缀公共子串，那么j++就行了，如果不相等那么就j=next[j]，这是什么意思呢

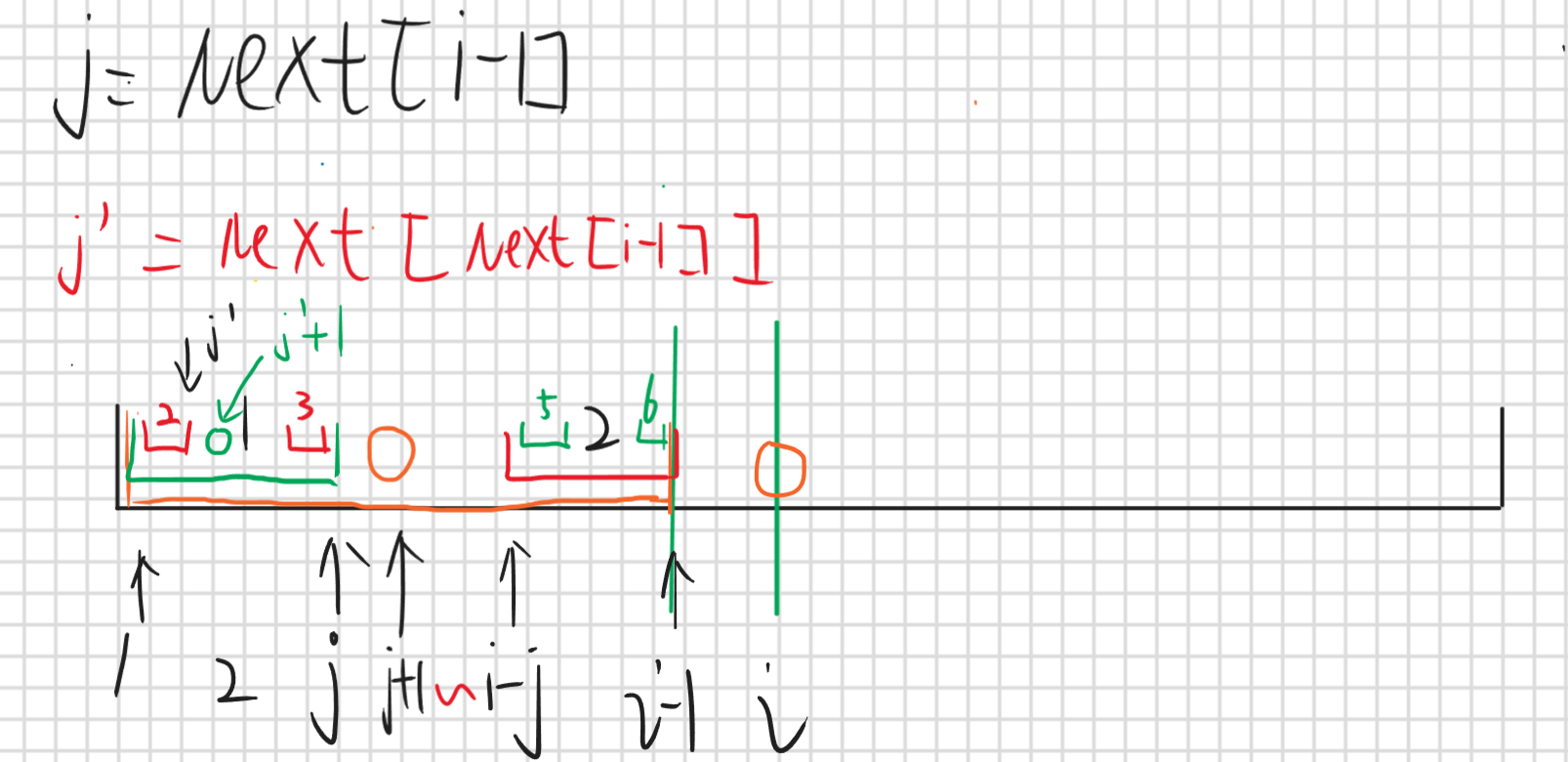
image.png

j更新成next[j]这里新的j用 j’ 表示，对应的公共前后缀子串就是区间2和区间3，因为区间1等于区间2所以区间2(p[1,j’])=区间3=区间5=区间6(p[i-j’,i-1])，那么如果p[j’+1]==p[i]那么就说明p[1,j’+1]==p[i-j’,i]那这就是最长公共前后缀子串，如果还是不相等那就继续j=Next[j]直到匹配成功或者j=0

代码

例题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<map>
using namespace std;
const int N =1e6+5;
char p[N],s[N];
int Next[N]; 
int main(){
	ios::sync_with_stdio(false);
	int n,m;
	cin>>n>>p+1>>m>>s+1;
	//求ne数组 ne[i]长度为i的模板串子串的公共前后缀字串长度 
	for(int i=2,j=0;i<=n;i++){
		while(j&&p[i]!=p[j+1])j=Next[j];
		if(p[i]==p[j+1])j++;
		Next[i]=j;
	}
	//kmp
	bool flag=true;
	for(int i=1,j=0;i<=m;i++){
		while(j&&s[i]!=p[j+1])j=Next[j];//匹配失败移动J指针到合理位置 
		if(s[i]==p[j+1])j++;
		if(j>=n){
			flag=false;
			cout<<i-n<<' ';
			j=Next[j];
		}
	} 
	
	if(flag) cout<<-1<<endl;
	

	return 0;
}