计算机图形学实验三《交互式绘制多边形》

这个只是先行版，最近比赛太多了有点忙不过来，讲得不好还请包含

视频讲解：咕咕咕~

一.交互式技术

人机交互就是指人与计算机之间使用某种对话语言，以一定的交互方式，为完成确定任务的人与计算机之间的信息交换过程。

1.消息响应函数

消息响应函数就是收到某些指定消息的时候，做出某些动作的函数，也叫消息处理函数。

有两种方法去添加消息响应函数一种是用户手动添加两个文件（（.h）和 (.cpp)）的内容，

一种就是用MFC自带的这里只说自带的且常用的。

消息响应函数有很多这里介绍常用的：

WM_LBUTTONDOWN//鼠标按下左键的消息
WM_LBUTTONUP//鼠标左键弹起的消息
//有左键就有右键和上面一样就是L换成R
WM_MOUSEMOVE//鼠标移动消息
//WM就是windows message的意思简单地说就比如第一个就是当你鼠标按下左键的时候
//就会做出对应的响应

接下来说一下如何添加

点击类向导然后

类名切换成你的View类如果你的项目叫Test那这个就是TestView类，然后点击消息，在那个搜索消息框里面搜索要添加的函数，点击之后右边现有处理程序框就会显示，然后点确定就好了。

以按下左键消息函数为例：

void CInteractionView::OnLButtonDown(UINT nFlags, CPoint point)
{
	// TODO: 在此添加消息处理程序代码和/或调用默认值
	CDC* pDC=GetDC();
	pDC->LineTo(point);
	CView::OnLButtonDown(nFlags, point);
}

这样写的意思就是当你按下左键的时候就会画一条直线，左键弹起就会小时，因为必须的按下左键才会显示导致我没法截图你们可以自己试试。

2.橡皮筋

这是我们想实现的结果，就是交互式的绘制多边形，大概思路就是用MouseMove(鼠标移动消息响应函数)去实现随着鼠标移动线向橡皮筋一样去实时的绘制，然后按下左键去确定点。

先看MouseMove

void CInteractionView::OnMouseMove(UINT nFlags, CPoint point)
{
	// TODO: 在此添加消息处理程序代码和/或调用默认值
	CDC* pDC = GetDC();
	pDC->LineTo(point);
	
	CView::OnMouseMove(nFlags, point);
}

这么写的意思就是移动到那线就画到哪那他就会这样

你会发现之前的线还在残留且不连续，假如你写个代码就绘制一条线那也会出现屏闪的情况

所以这里我们引入双缓冲技术

双缓冲

双缓冲是指一个显示缓冲区（显示设备上下文）和一个内存缓冲区（内存设备上下文）

在图形图像显示过程中，计算机从显示缓冲区取数据然后显示，很多图形的操作都很复杂需要大量的计算，很难访问一次显示缓冲区就能写入待显示的完整图形数据，通常需要多次访问显示缓冲区，每次访问时写入最新计算的图形数据。而这样造成的后果是一个需要复杂计算的图形，你看到的效果可能是一部分一部分地显示出来的，造成很大的闪烁不连贯。而使用双缓冲，可以使你先将计算的中间结果存放在另一个缓冲区中，但全部的计算结束，该缓冲区已经存储了完整的图形之后，再将该缓冲区的图形数据一次性复制到显示缓冲区

双缓冲就是用来解决单缓冲擦除图像时带来的屏幕闪烁问题

有些人可能会用SetROP2（R2_NOT）来实现这个原理就是清楚上一次绘制的案但毕竟不是我们自己写的所以这里我来讲如何自己实现双缓冲

现在TestView.h头文件(你的工程名字叫啥就是啥view)声明DoubleBuffer函数

然后再TestView.cpp源文件去实现对于函数代码

void CInteractionView::DoubleBuffer(CDC* pDC)//双缓冲
{
	CRect rect;//定义客户区
	GetClientRect(&rect);//获得客户区的大小
	CDC MemDC;//内存设备上下文
	CBitmap NewBitmap, * pOldBitmap;//内存中承载图像的临时位图
	MemDC.CreateCompatibleDC(pDC);//建立与屏幕pDC兼容的MemDC 
	NewBitmap.CreateCompatibleBitmap(pDC, rect.Width(), rect.Height());//创建兼容位图 
	pOldBitmap = MemDC.SelectObject(&NewBitmap); //将兼容位图选入MemDC 
	MemDC.FillSolidRect(rect, pDC->GetBkColor());//按原来背景填充客户区，否则是黑色 
	DrawObject(pDC);//这是我写的一个绘制图形的函数
	pDC->BitBlt(0, 0, rect.Width(), rect.Height(), &MemDC, 0, 0, SRCCOPY);//将内存位图拷贝到屏幕
	MemDC.SelectObject(pOldBitmap);//恢复位图
	NewBitmap.DeleteObject();//删除位图
	MemDC.DeleteDC();//删除MemDC
	ReleaseDC(pDC);//释放DC
}

这样就实现了双缓冲机制，代码都有注释不是什么高深的东西就是字面意思，不要想得太复杂也不用纠结调用的函数原理是啥你只需要知道他有啥用就行，如果看不懂注释的意思那就不要强求自己了你就当一个模板记住就行，要用的时候直接复制下来就行。

3.引力域

我们绘制的是一个封闭的多边形，但是最后要封闭的时候你很难精确的去点到那个起点那个像素点，所以我们这里引入引力域技术，效果就是在起点周围你点击鼠标他就会自动连上起点然后封闭。

很简单具体看我的OnLButtonDown函数

void CInteractionView::OnLButtonDown(UINT nFlags, CPoint point)
{
	// TODO: 在此添加消息处理程序代码和/或调用默认值
    //如果你有起点（其实这里应该判断至少有三个点才能封闭）然后鼠标当前点在起点
    //为中心边长为10像素的正方形时你点击就会自动连上起点形成封闭
	if (bLBDown && abs(point.x - P[0].x) <= 5 && abs(point.y - P[0].y) <= 5) {
		P[nCount] = P[0];//P[]数组是存所有点的，ncount是点的个数也是存当前点的下标
		is_Close = true;//is_Close用来判断封闭，这里封闭了所以将值改为true
	}
	else P[nCount++] = point;//如果没在那个范围就正常存点
	bLBDown = TRUE;//只要你点击了就肯定有起点了吗，这个就是用来判断是否有起点了
	
	CView::OnLButtonDown(nFlags, point);
}

那就说完了我把我的其他的代码发出来你们可以自己试试玩玩

OnMouseMove:

void CInteractionView::OnMouseMove(UINT nFlags, CPoint point)
{
	// TODO: 在此添加消息处理程序代码和/或调用默认值
	CDC* pDC = GetDC();
	if (bLBDown) {
		if (abs(point.x - P[0].x) <= 5 && abs(point.y - P[0].y) <= 5) {
			SetCursor(LoadCursor(NULL, IDC_HAND));//这一段的意思就是如果鼠标到
            //指定引力域了会将鼠标变成手指形状加强我们的人机交互体验
		}
	}
    
	if (!is_Close)P[nCount] = point;//只要没闭合就画线

	ReleaseDC(pDC);//释放DC
	Invalidate(FALSE);//不擦除背景
	
	CView::OnMouseMove(nFlags, point);
}

DrawObject：

void CInteractionView::DrawObject(CDC* pDC)//绘制多边形
{
	pDC->SelectStockObject(GRAY_BRUSH);//画刷设置为灰色等会说为啥要用画刷
    //P[]是一个CPoint数组存了我要绘制的点
    //这个代码就是把P数组存的点用线连接绘制出来
	for (int i=0;i<=nCount;i++) {
		if (!i) {//P[0]是起点所以是MoveTo先移动到第一个点
			pDC->MoveTo(P[i]);
		}
		else pDC->LineTo(P[i]);//其余点就直接画过去就行
	}

	if (bLBDown) {//如果bLBDown为真就说明第一个点确定了
		pDC->Rectangle(P[0].x - 5, P[0].y - 5, P[0].x + 5, P[0].y + 5);
        //在第一个点绘制一个灰色的矩形，这个矩形就是引力域范围等会就说
	}
	
}

到这里就实现了交互式绘制多边形

二.有效边表填充算法

也可以说是y向连贯性算法，有效边表填充算法就是对x扫描线的一个优化，这个可能理解有点困难如果你的c/c++基础很差，数据结构也不会，指针概念模糊，那可能这里很难听懂，对此我建议开摆多看几遍我会把这些你们没学遗漏的知识讲一遍。不过有一说一这个确实先对来说难，比起种子填充算法来说，种子填充就是个简单的BFS或者DFS搜索涉及的前置知识不多。

1.X扫描线算法

X-扫描线算法一共就四步：

求交: 确定扫描线和多边形的交点
排序：把所有交点按递增顺序排序（按交点x值递增排序，确保交点两两配对时填充区间的正确性）
配对：确定填充区间
着色：着色规则有说法的，就我拿一个bool flag初始化为false,这个flag如果为false表示在多边形外面否则在里面，一开始为false，当你碰到一个交点的时候就代表从外进入到内，所以将flag=true,只要flag为true就涂色，因为当你碰到一个交点那你肯定要么是从外到内要么就是内到外，所以状态改变一下就好了

边界像素处理原则：

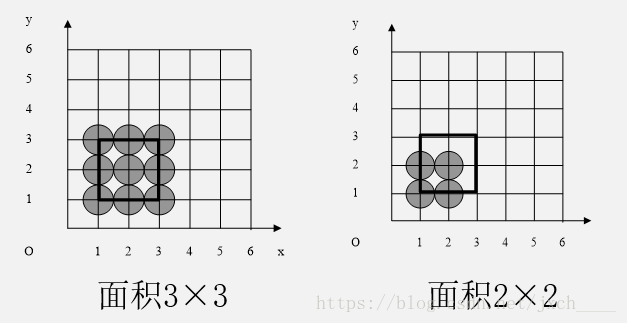
这里写图片描述

假设你要填充的是黑色正方形，那对于边界上的点该怎么取舍呢，如果你边界上的点全涂色，那就是左边那个图的情况，那肯定是不对的因为你要涂色的图形才2x2大小而你画的是个3x3大小的，我们这里采用的是左闭右开，上闭下开原则

对于顶点到底是算一个还是算两个呢，如果算一个那看上面那个多边形图的红色扫平描线，如果算一个点，那么红色扫描小经过p3的时候flag就会变成true那么他就会把(p3,p5)区间填充颜色，那就错了，那假如顶点算两个点那你看紫色扫描线，当她经过p2点的时候flag因为经过两个点就还是false,那么就不会填充p2到边界这段，那也错了，那该如何处理这种情况呢，处理办法就是这个顶点上面有多少条边就把他当几个点。你这么想如果它上面没有边或者有两条边那他肯定是尖尖，所以y方向上是不需要填充的，如果只有一条边，那他的y方向上就需要填充。

2.指针

因为接下来要讲的链表和有效边表算法都涉及到指针，担心有些同学指针概念模糊不会用这里还是简单讲一下，因为指针用了要是用不好后果还是很可怕的有时候。

我们知道C/C++的变量存放在内存中，而内存其实就是一组有序字节组成的数组，每个字节有唯一的内存地址。CPU 通过内存寻址对存储在内存中的某个指定数据对象的地址进行定位。这里，数据对象是指存储在内存中的一个指定数据类型的数值或字符串，它们都有一个自己的地址，而指针便是保存这个地址的变量。也就是说：指针是一种保存变量地址的变量。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N =1e6+5;

int main(){
	ios::sync_with_stdio(false);
	int* a=NULL;//声明一个 int 类型的指针 a 
	char *b=NULL;//声明一个 char 类型的指针 b,*这个跟谁挨着都行
	//指针一定要初始化如果一个指针没有被初始化，那么程序就不知道它指向哪里。
	//它可能指向一个非法地址，这时，程序会报错 
	int x=10;
	a=&x; //&是取地址符，也就是将存储x变量的地址给了a 
	
	cout<<"x变量的地址:"<<a<<endl;//输出看一看
	cout<<"a地址存放的数据："<<*a<<endl;
	int** p=&a;//也可以二级指针 去指向指针
	cout<<"a指针的地址:"<<p<<endl;//输出看一看
	cout<<"p地址存放的数据："<<*p<<endl;
	return 0;
}

指针也可以进行加减还有很多关于指针的东西，但这里就不说了感兴趣可以自己网上查查，这里至少简单了解一下指针，不然接下来会不好理解。

3.链表

因为接下来说的几种数据结构都涉及到了链表的思路如果你会那就忽略这里

链表是一种这样的数据结构，其中的对象按线性顺序排列。数组的线性顺序是由数组下标决定的，然而与数组不同的是，链表的顺序是由各个对象的指针决定的。链表为动态集合提供了一种简单且灵活的表示方法。相对于数组，链表优点是使用直观，便于快速、随机地存取线性表中的任一元素，但缺点是对其进行插入和删除操作时需要移动大量的数组元素，同时由于数组属于静态内存分配，定义数组时必须指定数组的长度，程序一旦运行，其长度就不能再改变，实际使用个数不能超过数组元素最大长度的限制，否则就会发生下标越界的错误，低于最大长度时又会造成系统资源的浪费，因此空间效率差。

这里就介绍一下单链表的组成，插入，查找，删除等操作，主要是有链表得这么一个概念。

链表组成部分就两部分

数据域就存储该节点对应的数据内容，而指针域就是储存下一个节点的指针。

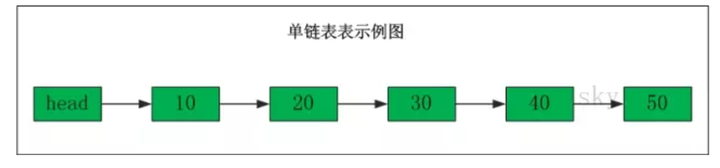
接下来看一下具体代码咋写，不理解的我在下面放了图示可以和注释一起帮助理解，如果还是不理解也可以网上看看别人的讲解，我讲的也不好。

#include <iostream>
using namespace std;
struct Link{//定义链表结构体
	//数据域
	int  data;
	//指针域
    Link *Next;//(c++ 在创建结构体变量的时候可以省略struct关键字，c不行)
    //像这种只有一个指针域的就是单链表
};
int main(){
	ios::sync_with_stdio(false);//关闭源流同步不重要忽略

    Link * p = (Link*)malloc(sizeof(Link));//创建一个头结点
    Link * temp = p;//声明一个指针指向头结点，用于遍历链表
    int i = 0;
    //生成链表
    for (int i = 0; i < 5; i++) {
        //创建节点并初始化
        Link *a = (Link*)malloc(sizeof(Link));
        a->data = i;
        a->Next = NULL;
        //建立新节点与直接前驱节点的逻辑关系
        temp->Next = a;
        temp = temp->Next;
    }
    //遍历输出链表，也可以实现查找操作
    cout<<"输出链表:"<<endl; 
    temp=p;//将temp指向头节点 
    while(temp->Next!=NULL){//如果节点的下一个节点不为空 则一直循环下去知道为空 
    	cout<<temp->Next->data<<' ';//则输出节点下一个节点的数据 
    	temp=temp->Next;//移动节点到下一个节点 
	}
	cout<<endl;
    //删除结点数据为3的结点
	int val=3;
	Link *del;//存储删除结点的地址 
	temp=p;
	while(temp->Next!=NULL){//如果节点的下一个节点不为空 则一直循环下去知道为空 
    	if(temp->Next->data==val){
    		del=temp->Next;
    		temp->Next=temp->Next->Next;
    		free(del);//释放内存为了防止内存泄漏的发生，须及时调用free（）释放已不再使用的内存 
    		break;
		}
    	temp=temp->Next;//移动节点到下一个节点 
	}
	cout<<"删除结点为3的结点后的链表："<<endl;
	temp=p;//将temp指向头节点 
    while(temp->Next!=NULL){//如果节点的下一个节点不为空 则一直循环下去知道为空 
    	cout<<temp->Next->data<<' ';//则输出节点下一个节点的数据 
    	temp=temp->Next;//移动节点到下一个节点 
	}
	
	 
	return  0;
}

运行结果：

链表中插入元素的 3 种情况示意图

链表删除元素示意图

4.有效边表

如果一条扫描线我们每条边都去和他进行求交，那会很麻烦，就比如我们对n边型进行求交那就是O(N)的时间复杂度，就是要求N次交10000条边就是10000次，那会很慢，我们只需要对有效边去求交就行了，有效边就是和扫描线与交点的边，为此我们建立有效边表这一数据结构。

数据结构就是存储，组织数据的一种方式，说简单点就是以一种特定的形式去存储一些数据，来达到优化的目的，99%的数据结构都是拿来优化的。

有效边表的格式：

这里写图片描述

class CAET
{
public:
	CAET();
	virtual ~CAET();
public:
	double  x;//当前扫描线与有效边交点的x坐标
	int     yMax;//边的最大y值
	double  k;//斜率的倒数(x的增量)
	Point1  ps;//边的起点
	Point1  pe;//边的终点
	CAET* pNext;
};

其中x就是有效边与扫描线的交点的x坐标，ymax就是这条边最大的y坐标，1/k是该直线的斜率倒数，next是下一条边的结点指针

引入有效边表的目的是为了方便我们去计算扫描线与边的交点，我们可以根据之前所学的直线算法的分量思想去推算出下一条扫描线与该边的交点，简单地说就是我们让y坐标+1，这样x坐标只需要去加1/k，这样我们就可以根据有效边表去高效的计算出扫描线与有效边的交点

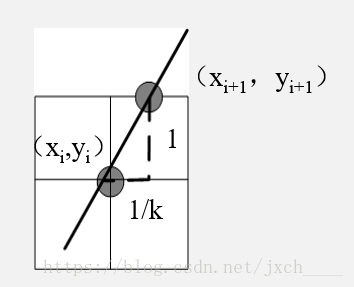
这里写图片描述

可以根据计算机图形学书P118有效边表的建立过程自己模拟一遍，这里就不赘述了。

5.桶表和边表

不过这里又有一个问题，我们虽然可以高效的计算出扫描线与有效边的交点，但是我们不知道什么时候让有效边插入，就是我们不知道什么时候去和某一条有效边去进行求交，所以我们这里引入了桶表和边表，边表用以存放多边形上各条边出现的信息，因为水平边斜率倒数是无穷大且水平边就是扫描线所以不做考虑。

桶表大概就是这样：

class CBucket  
{
public:
	CBucket();
	virtual ~CBucket();
public:
	int     ScanLine;     //扫描线
	CAET    *pET;         //桶上的边表指针
	CBucket *pNext;		  //桶表的下一个的指针
};

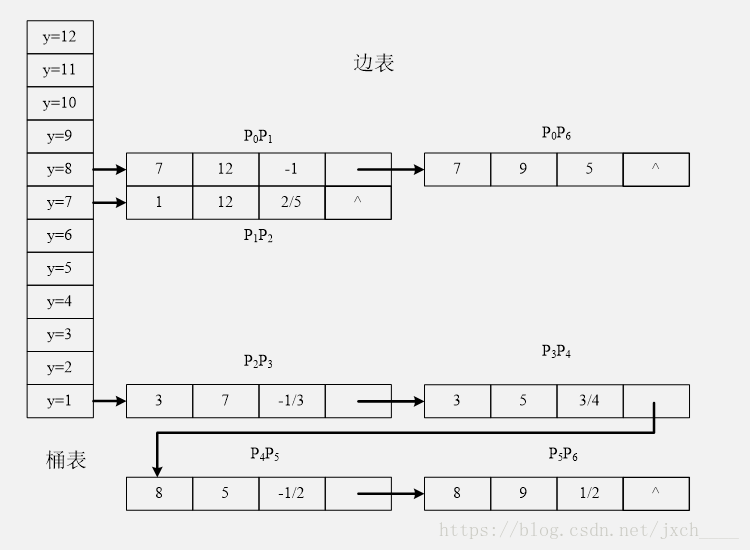
你可以理解为桶表就是所有扫描线的集合，然后每条扫描线都有一个边表指针表示在该桶表节点上的边表，这里边表的插入就类似于链表，桶表本身就是链表只是在它的每一个节点上又去接上了一个边表，将每条边的信息（也就是边表）链入与该边最小y坐标（ymin）相对应的桶处。也就是说，若某边的较低端点为ymin，则该边就存放在相应的扫描线桶中。
对于每一条扫描线，如果新增多条边，则按x|ymin（较低端的x坐标）坐标递增的顺序存放在一个链表中，若x|ymin 相等，则按照1/k由小到大排序（接下来就会讲如何排序），这样就形成边表，（不存在x相等，k还想等情况）。

可以配合图来理解

这是边表，结构其实类似于有效边表，所以可以和有效边表用一个类来表示，存放的是一条边较低端的端点x坐标（用来判断边表在桶中的排序），和最高端的y坐标（用来判断有效边何时无效），以及斜率倒数。

这里写图片描述

这是桶表和边表这样看上去就很好理解了

这里写图片描述

6.动态链表冒泡排序

刚刚也提到了排序，我们要对边表进行一个排序，为啥要排序，是因为我们要填充颜色，我们要先配对确定填充空间，然后填色，忘了的可以看看上面说的那四个步骤，排序规则是x小在前面，如果一样那就比斜率倒数，不存在x和斜率都相等的情况，因为我们排序的边表有个前提条件就是y坐标相同因为在同一条扫描线上。

那怎么对动态链表排序呢，这里有很多方法，这里说一个最简单不过效率也是最低的冒泡排序，其实我认为这里用堆来优化应该是最好的，因为堆是没插入一个新的东西才会up(),down(),效率每次都是log(N),总共就是Mlog(N)，但是其他log级别排序比如快排，是每次都是Nlog(N)总的算下来应该是NMlog(N),,而冒泡本身是N^2,排序M次则是M*N^2,不过优点就是很稳定。对于排序我的B站有相关讲解感兴趣的可以去看看然后自己试着去优化，这里先讲冒泡。

先看一下冒泡排序的流程：

在这里插入图片描述

简单地说就是她一共是两层循环，外层是确定排序位置，内部进行相邻比较，就是

//这里写的不一定对就是表述一下排序思路，从小到大排序
for(int i=0;i<n;i++){
    外部是确定位置就当i等于0的时候那进行完内部循环数组下标为0的点就是正确排序的点
	for(int j=i;j+1<n;j++){
        if(j>j+1)swap(j,j+1);//相邻点比较大了就交换
	}
}

要是不理解冒泡排序的思路可以看一下别人的博客或者视频不难，我主要说动态链表的排序，其实这里最好视频讲但现在没时间

void CFill::ETOrder()//边表的冒泡排序算法
{

	CAET* pT1 = NULL, * pT2 = NULL;//CAET是边表类，创建了两个指针
	int Count = 1;//计数的
	pT1 = pHeadE;//pHeadE是头指针，pT1指向头指针
	if (pT1 == NULL)
	{
		return;//如果头指针为空则说明没东西不需要排序直接返回
	}
	if (NULL == pT1->pNext)
	{
		return;//如果头指针下一个为空则说明就一个那也不需要排序直接返回
	}
	while (NULL != pT1->pNext)//遍历统计结点数
	{
		Count++;//统计结点数
		pT1 = pT1->pNext;
	}
	for (int i = 1; i < Count; i++)//外部循环确定正确排序下标
	{
		pT1 = pHeadE;//pT1重置为头指针      
		if (pT1->x > pT1->pNext->x || (pT1->x == pT1->pNext->x && pT1->k > pT1->pNext->k))
		{
            // ||前半段是该节点的x坐标如果比下一个节点大那就要交换
            //下半段就是如果x坐标相等但是k大的话也要交换
            //交换步骤，交换pt1和Pt1下一个节点
			pT2 = pT1->pNext;//pt2存一下pt1下一个节点
			pT1->pNext = pT1->pNext->pNext;//这里看一下我上面说的链表，让pt1下一个节点指向pt2的下一个
			pT2->pNext = pT1;//然后再让pt2下一个指向pt1
			pHeadE = pT2;//头指针更新为pt2
		}
        //因为第一次如果交换了则会涉及头指针的变换，所以上面是第一次交换做了特判接下来就是遍历到底
		pT1 = pHeadE;//重置为头指针
		while (pT1->pNext->pNext != NULL)//如果下一个的下一个为空就结束，因为要比的就是下一个和下下一个
		{
			pT2 = pT1;//pt2存Pt1
			pT1 = pT1->pNext;//pt1存pt1下一个，
			if (pT1->x > pT1->pNext->x || (pT1->x == pT1->pNext->x && pT1->k > pT1->pNext->k))
			{	//和上面一样的判断是否需要交换
				pT2->pNext = pT1->pNext;
				pT1->pNext = pT1->pNext->pNext;
				pT2->pNext->pNext = pT1;
				pT1 = pT2->pNext;
			}
		}
	}

}

这样就排序完了

7.总流程

首先一共就四步，其他的什么桶表边表都是用来辅助优化的。

求交: 确定扫描线和多边形的交点
排序：把所有交点按递增顺序排序（按交点x值递增排序，确保交点两两配对时填充区间的正确性）
配对：确定填充区间
着色：着色规则有说法的，就我拿一个bool flag初始化为false,这个flag如果为false表示在多边形外面否则在里面，一开始为false，当你碰到一个交点的时候就代表从外进入到内，所以将flag=true,只要flag为true就涂色，因为当你碰到一个交点那你肯定要么是从外到内要么就是内到外，所以状态改变一下就好了

为了加快求交速度引入了有效边，为了知道何时插入有效边，且帮助排序引入了，桶表和边表，排序算法也是为了优化排序速度和稳定性，配对就是两两配对就是边界顶点根据点上面的有效边数确定它到底算几个点，然后就是着色。

这是我fill.h就是实现填充的

#pragma once
#include "Bucket.h"
#include"Point1.h"
class CFill
{
public:
	CFill();
	virtual ~CFill();
	void SetPoint(Point1* p, int);//初始化
	void CreateBucket();//创建桶
	void CreateEdge();//边表
	void AddET(CAET*);//合并ET表
	void ETOrder();//ET表排序
	void Gouraud(CDC*);//填充多边形
	void ClearMemory();//清理内存
	void DeleteAETChain(CAET* pAET);//删除边表
protected:
	int     PNum;//顶点个数
	Point1* P;//顶点坐标动态数组
	CAET* pHeadE, * pCurrentE, * pEdge; //有效边表结点指针
	CBucket* pHeadB, * pCurrentB;        //桶表结点指针
};

fill.cpp源文件

#include "pch.h"
#include "Fill.h"
#define Round(f) int(floor(f+0.5))
CFill::CFill()//构造函数初始化
{
	PNum = 0;
	P = NULL;
	pEdge = NULL;
	pHeadB = NULL;
	pHeadE = NULL;
}

CFill::~CFill()//析构函数
{
	if (P != NULL)
	{
		delete[] P;
		P = NULL;
	}
	ClearMemory();
}

void CFill::SetPoint(Point1* p, int m)//将我们的多边形点数组转存到P
{
	P = new Point1[m];//创建一维动态数组
	for (int i = 0; i < m; i++)
	{
		P[i]=p[i];
	}
	PNum = m;
}

void CFill::CreateBucket()//创建桶表
{
	int yMin, yMax;
	yMin = yMax = P[0].y;
	for (int i = 0; i < PNum; i++)//查找多边形所覆盖的最小和最大扫描线
	{
		if (P[i].y < yMin)
		{
			yMin = P[i].y;//扫描线的最小值
		}
		if (P[i].y > yMax)
		{
			yMax = P[i].y;//扫描线的最大值
		}
	}
	for (int y = yMin; y <= yMax; y++)
	{
		if (yMin == y)//如果是扫描线的最小值
		{
			pHeadB = new CBucket;//建立桶的头结点
			pCurrentB = pHeadB;//pCurrentB为CBucket当前结点指针
			pCurrentB->ScanLine = yMin;
			pCurrentB->pET = NULL;//没有链接边表
			pCurrentB->pNext = NULL;
		}
		else//其他扫描线
		{
			pCurrentB->pNext = new CBucket;//建立桶的其他结点
			pCurrentB = pCurrentB->pNext;
			pCurrentB->ScanLine = y;
			pCurrentB->pET = NULL;
			pCurrentB->pNext = NULL;
		}
	}
}

void CFill::CreateEdge()//创建边表
{
	for (int i = 0; i < PNum; i++)
	{
		pCurrentB = pHeadB;
		int j = (i + 1) % PNum;//边的另一个顶点，P[i]和P[j]点对构成边
		if (P[i].y < P[j].y)//边的终点比起点高
		{
			pEdge = new CAET;
			pEdge->x = P[i].x;//计算ET表的值
			pEdge->yMax = P[j].y;
			pEdge->k = (P[j].x - P[i].x) / (P[j].y - P[i].y);//代表1/k
			pEdge->ps = P[i];//绑定顶点和颜色
			pEdge->pe = P[j];
			pEdge->pNext = NULL;
			while (pCurrentB->ScanLine != P[i].y)//在桶内寻找当前边的yMin
			{
				pCurrentB = pCurrentB->pNext;//移到yMin所在的桶结点
			}
		}
		if (P[j].y < P[i].y)//边的终点比起点低
		{
			pEdge = new CAET;
			pEdge->x = P[j].x;
			pEdge->yMax = P[i].y;
			pEdge->k = (P[i].x - P[j].x) / (P[i].y - P[j].y);
			pEdge->ps = P[i];
			pEdge->pe = P[j];
			pEdge->pNext = NULL;
			while (pCurrentB->ScanLine != P[j].y)
			{
				pCurrentB = pCurrentB->pNext;
			}
		}
		if (P[i].y != P[j].y)
		{
			pCurrentE = pCurrentB->pET;
			if (pCurrentE == NULL)
			{
				pCurrentE = pEdge;
				pCurrentB->pET = pCurrentE;
			}
			else
			{
				while (pCurrentE->pNext != NULL)
				{
					pCurrentE = pCurrentE->pNext;
				}
				pCurrentE->pNext = pEdge;
			}
		}
	}
}

void CFill::Gouraud(CDC* pDC)//填充多边形
{
	CAET* pT1 = NULL, * pT2 = NULL;
	pHeadE = NULL;
	for (pCurrentB = pHeadB; pCurrentB != NULL; pCurrentB = pCurrentB->pNext)
	{
		for (pCurrentE = pCurrentB->pET; pCurrentE != NULL; pCurrentE = pCurrentE->pNext)
		{
			pEdge = new CAET;
			pEdge->x = pCurrentE->x;
			pEdge->yMax = pCurrentE->yMax;
			pEdge->k = pCurrentE->k;
			pEdge->ps = pCurrentE->ps;
			pEdge->pe = pCurrentE->pe;
			pEdge->pNext = NULL;
			AddET(pEdge);
		}
		ETOrder();
		pT1 = pHeadE;
		if (pT1 == NULL)
			return;
		while (pCurrentB->ScanLine >= pT1->yMax)//下闭上开
		{
			CAET* pAETTEmp = pT1;
			pT1 = pT1->pNext;
			delete pAETTEmp;
			pHeadE = pT1;
			if (pHeadE == NULL)
				return;
		}
		if (pT1->pNext != NULL)
		{
			pT2 = pT1;
			pT1 = pT2->pNext;
		}

		while (pT1 != NULL)
		{
			if (pCurrentB->ScanLine >= pT1->yMax)//下闭上开
			{
				CAET* pAETTemp = pT1;
				pT2->pNext = pT1->pNext;
				pT1 = pT2->pNext;
				delete pAETTemp;
			}
			else
			{
				pT2 = pT1;
				pT1 = pT2->pNext;
			}
		}
		BOOL bInFlag = FALSE;//区间内外测试标志，初始值为假表示区间外部
		double xb, xe;//扫描线与有效边相交区间的起点和终点坐标
		for (pT1 = pHeadE; pT1 != NULL; pT1 = pT1->pNext)
		{
			if (FALSE == bInFlag)
			{
				xb = pT1->x;
				bInFlag = TRUE;
			}
			else
			{
				xe = pT1->x;
				for (double x = xb; x < xe; x++)//左闭右开
				{
					pDC->SetPixelV(Round(x), pCurrentB->ScanLine, RGB(255,0,0));
				}
				bInFlag = FALSE;
			}
		}
		for (pT1 = pHeadE; pT1 != NULL; pT1 = pT1->pNext)//边的连续性
		{
			pT1->x = pT1->x + pT1->k;
		}
	}
}

void CFill::AddET(CAET* pNewEdge)//合并ET表
{
	CAET* pCE = pHeadE;
	if (pCE == NULL)
	{
		pHeadE = pNewEdge;
		pCE = pHeadE;
	}
	else
	{
		while (pCE->pNext != NULL)
		{
			pCE = pCE->pNext;
		}
		pCE->pNext = pNewEdge;
	}
}

void CFill::ETOrder()//边表的冒泡排序算法
{

	CAET* pT1 = NULL, * pT2 = NULL;
	int Count = 1;
	pT1 = pHeadE;
	if (NULL == pT1)
	{
		return;
	}
	if (NULL == pT1->pNext)
	{
		return;
	}
	while (NULL != pT1->pNext)
	{
		Count++;
		pT1 = pT1->pNext;
	}
	for (int i = 1; i < Count; i++)
	{
		pT1 = pHeadE;
		if (pT1->x > pT1->pNext->x || (pT1->x == pT1->pNext->x && pT1->k > pT1->pNext->k))
		{
			pT2 = pT1->pNext;
			pT1->pNext = pT1->pNext->pNext;
			pT2->pNext = pT1;
			pHeadE = pT2;
		}
		pT1 = pHeadE;
		while (pT1->pNext->pNext != NULL)
		{
			pT2 = pT1;
			pT1 = pT1->pNext;
			if (pT1->x > pT1->pNext->x || (pT1->x == pT1->pNext->x && pT1->k > pT1->pNext->k))
			{
				pT2->pNext = pT1->pNext;
				pT1->pNext = pT1->pNext->pNext;
				pT2->pNext->pNext = pT1;
				pT1 = pT2->pNext;
			}
		}
	}

}

void CFill::ClearMemory()//安全删除所有桶与桶上连接的边
{
	DeleteAETChain(pHeadE);
	CBucket* pBucket = pHeadB;
	while (pBucket != NULL)//针对每一个桶
	{
		CBucket* pBucketTemp = pBucket->pNext;
		DeleteAETChain(pBucket->pET);
		delete pBucket;
		pBucket = pBucketTemp;
	}
	pHeadB = NULL;
	pHeadE = NULL;
}

void CFill::DeleteAETChain(CAET* pAET)
{
	while (pAET != NULL)
	{
		CAET* pAETTemp = pAET->pNext;
		delete pAET;
		pAET = pAETTemp;
	}
}

计算机图形学实验三《交互式绘制多边形》

计算机图形学实验三《交互式绘制多边形》

这个只是先行版，最近比赛太多了有点忙不过来，讲得不好还请包含

视频讲解：咕咕咕~

一.交互式技术

1.消息响应函数

2.橡皮筋

双缓冲

3.引力域

OnMouseMove:

DrawObject：

二.有效边表填充算法

1.X扫描线算法

X-扫描线算法一共就四步：

边界像素处理原则：

2.指针

3.链表

4.有效边表

5.桶表和边表

6.动态链表冒泡排序

7.总流程

三.种子填充算法

1.DFS(栈)

2.BFS（队列）

3.基础剪枝

计算机图形学实验三 《交互式绘制多边形》

这个只是先行版，最近比赛太多了有点忙不过来，讲得不好还请包含

视频讲解：咕咕咕~

一.交互式技术

1.消息响应函数

2.橡皮筋

双缓冲

3.引力域

OnMouseMove:

DrawObject：

二.有效边表填充算法

1.X扫描线算法

X-扫描线算法一共就四步：

边界像素处理原则：

2.指针

3.链表

4.有效边表

5.桶表和边表

6.动态链表冒泡排序

7.总流程

三.种子填充算法

1.DFS(栈)

2.BFS（队列）

3.基础剪枝

计算机图形学实验三《交互式绘制多边形》