kmp实际就是一种字符串查找算法，一般数据的时候我们可以直接暴力匹配但对于大数据是行不通的，接下来我以s为母串p为目标字符串。

图片.png

　　如上图只有最后一位p[6]匹配失败按照传统暴力办法则要往后移动一位再继续匹配，就是这样

图片.png

　　这样是十分浪费时间的因为在之前的匹配中我们已经知道s[5]=p[1]，而p[1]肯定不等于p[0]所以s[5]肯定不等于p[0]，而kmp就是利用之前已经

部分匹配这个有效信息，保持i 不回溯，通过修改j 的位置，让模式串尽量地移动到有效的位置。

　　KMP:

　　先说定义吧什么是KMP,

　　假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

  • 如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；
  • 如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。
  • 换言之，当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值，即**移动的实际位数为：j - next[j]**，且此值大于等于1。

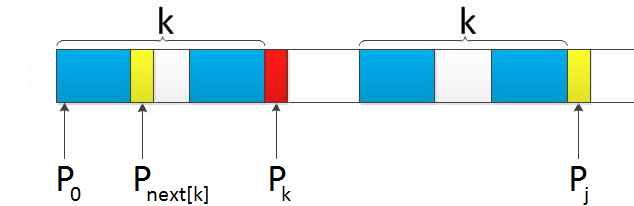
　　而next数组的含义就是比如next[j]表示的就是在长度为j-1的p目标字符串中最长的相同前缀和后缀长度。

　　也就是说在上图得情况中我们没必要这么一步一步往后推而是这样

图片.png

　　因为next数组的定义就是长度为j-1的目标字符串最大相同前缀后缀长度，所以往后移动j-next[j]就可以让其移动到一个效率跟高的位置，为什么呢，因为

在我们匹配的时候已经知道前j-1是已经匹配好的，那我们以前j-1字符串的前缀为基点移动到和他相同的最长后缀就可以了。

　　思路很好理解问题就是next数组该怎么求　

　　next数组：

　　next数组的定义就是next[j]表示的就是在长度为j-1的p目标字符串中最长的相同前缀和后缀长度，所以我们只需要找到每个位置最长前缀后缀，然后整体

右移一位赋初值为-1就可以了。这就是求next的思路，继续分析，假设我们已经知道了next[j]去求next[j+1]，假设next[j]就等于k，也就是在j-1的目标字符串中

前缀和后缀相同最长长度为k，那我们只需要去比较p[k]和p[j]就可以了，因为p0pk-1是和pj-kpj-1是相同的，如果pk==pj那么next[j+1]=next[j]+1=k+1,那假如不同呢？

　　不同的情况我们这样去理解：

　　先说结论就是去递归k=next[k]直到pk‘==pj然后next [j + 1] = k’ + 1 = next [k’ ] + 1，或者找不到就为0。那为什么是去递归k=next[k]呢，我们继续从next的定义出发，对于pj+1目标字符串来说他只是p[k]!=p[j]但是p0pk-1是和pj-kpj-1是相同的，从效率上讲我们只需要去找一个和p0pk-1相同的前缀然后最后一位和pj相同就是我们要的值，而和p0pk-1相同的前缀就是p0~p[next[k]]-1，不懂可以再看一下next数组的定义，所以我们只需要去比较p[next[k]]和p[j]是否相同就可以了相同就next [j + 1] = k’ + 1 = next [k’ ] + 1，不同就继续递归索引直到没有然后值就是0。

图片.png

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<stdio.h>
#include<string.h>
char a[1000005],b[1000005];
int next[1000005];
void getnext(int len);
int kmp(int l1,int l2);
int main(){
    int sum;
    while(~scanf("%s %s",&a,&b)){
        sum=kmp(strlen(a),strlen(b));
        if(sum>=0)
        printf("%d\n",sum);
        else
        printf("-1\n");
    }
    return 0;
} 
void getnext(int len){
    int i=0,j=-1;
    next[0]=-1;
    while (i < len)
    {
        if (j == -1 || b[i] == b[j])
        {
            ++i;
            ++j;
            next[i] = j;
  
        }    
        
        else
            j=next[j];
    }
}
int kmp(int l1,int l2){
    int i=0,j=0;
    getnext(l2);
    while(i<l1&&j<l2){
        if(j==-1||a[i]==b[j]){
            i++;
            j++;    
        }
        else
            j=next[j];    
    }
    if(j>=l2)
        return i-l2;
    else 
        return -1;
}

　但其实这个代码还有一点点小问题，就是这种情况

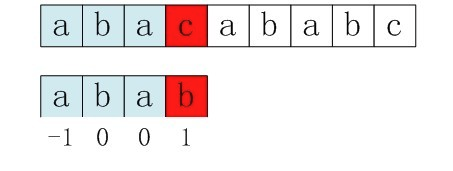
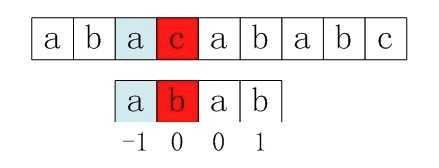
图片.png

图片.png

　　按照我们kmp的作用来说不应该出现这种失匹的情况，为什么会发生呢，问题出在不该出现p[j] = p[ next[j] ]。为什么呢？理由是：当p[j] != s[i] 时，下次匹配必然是p[ next [j]] 跟s[i]匹配，如果p[j] = p[ next[j] ]，必然导致后一步匹配失败（因为p[j]已经跟s[i]失配，然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配，很显然，必然失配），所以**不能允许p[j] = p[ next[j ]]**。如果出现了p[j] = p[ next[j] ]咋办呢？如果出现了，则需要再次递归，即令next[j] = next[ next[j] ]。

　　所以优化一下的代码就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<stdio.h>
#include<string.h>
char a[1000005],b[1000005];
int next[1000005];
void getnext(int len);
int kmp(int l1,int l2);
int main(){
    int sum;
    while(~scanf("%s %s",&a,&b)){
        sum=kmp(strlen(a),strlen(b));
        if(sum>=0)
        printf("%d\n",sum);
        else
        printf("-1\n");
    }
    return 0;
} 
void getnext(int len){
    int i=0,j=-1;
    next[0]=-1;
    while (i < len)
    {
        if (j == -1 || b[i] == b[j])
        {
            ++i;
            ++j;
            if(b[i]!=b[j])
                next[i] = j;
            else
                next[i]=next[j];    
        }    
        
        else
            j=next[j];
    }
}
int kmp(int l1,int l2){
    int i=0,j=0;
    getnext(l2);
    while(i<l1&&j<l2){
        if(j==-1||a[i]==b[j]){
            i++;
            j++;    
        }
        else
            j=next[j];    
    }
    if(j>=l2)
        return i-l2;
    else 
        return -1;
}